Định giá chứng quyền như thế nào?

Chia sẻ trên:    15795

Định giá chứng quyền như thế nào luôn là câu hỏi lớn được quan tâm của các nhà đầu tư. Bài viết này sẽ giúp quý nhà đầu tư tiếp cận cách định giá chứng quyền thông qua mô hình Black-Scholes.

Video: Cách định giá chứng quyền

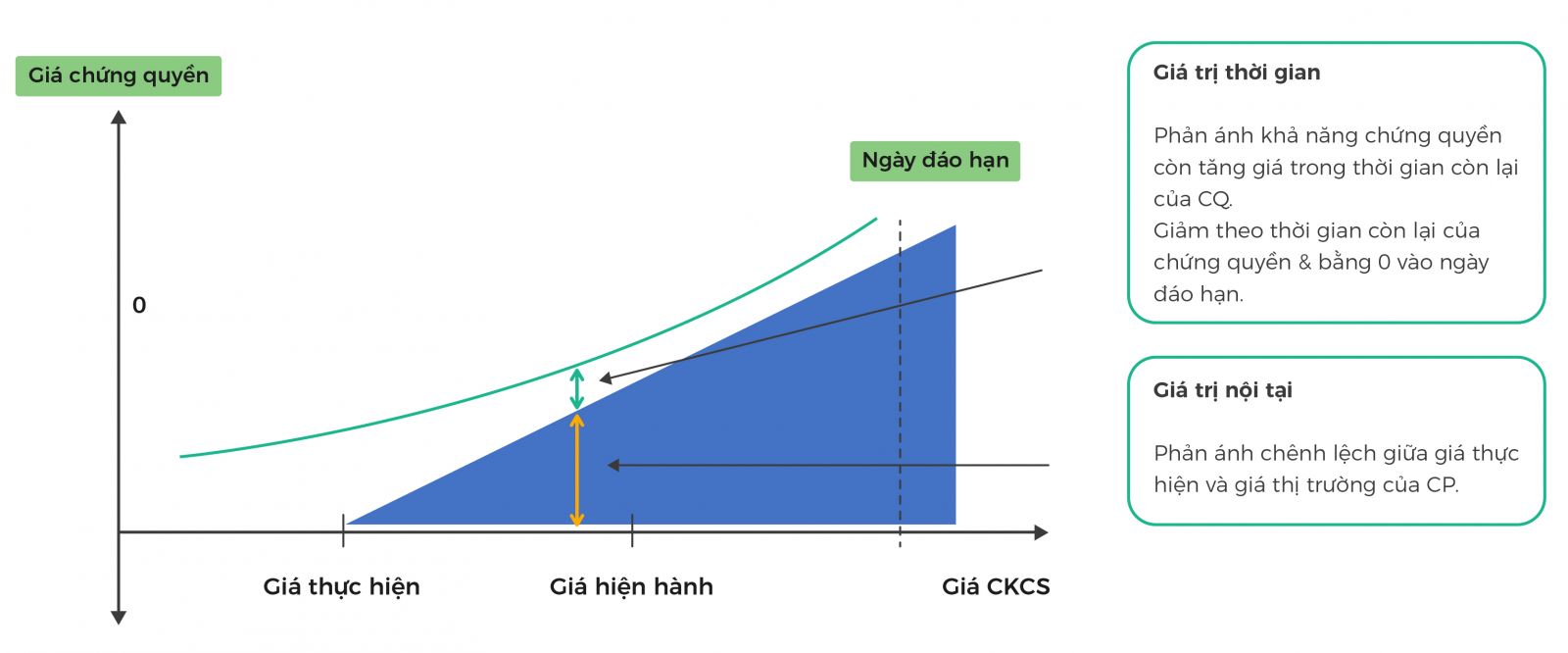
Cấu trúc giá của một chứng quyền có bảo đảm

Theo lý thuyết, giá của một chứng quyền bảo đảm khi chưa đáo hạn bao gồm hai phần: giá trị nội tại và giá trị thời gian, trong đó:

Định giá chứng quyền bằng mô hình Black-Scholes

Mô hình định giá quyền chọn của Black-Scholes phát triển năm 1973 đã giúp đẩy mạnh các giao dịch quyền chọn. Mô hình có thể lập trình trên các bảng tính hoặc trên các máy tính tài chính. Mô hình xuất phát từ quan niệm phòng ngừa hoàn toàn rủi ro, là kiểu phòng ngừa bằng cách mua một cổ phiếu và tiến hành bán ngay quyền chọn mua cổ phiếu đó và kết quả là không có rủi ro.

Để xác định giá của một chứng quyền. Mô hình Black-Scholes sẽ cho phép chúng ta xác định giá trị tương đối của một option (quyền chọn). Với công thức tính toán như sau:

Giá quyền chọn mua: 

Giá quyền chọn bán: 

Trong đó:

So: Giá hiện tại của TSCS

K: Giá thực hiện chứng quyền

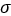: Độ biến động giá kỳ vọng của TSCS

r: lãi suất phi rủi ro

t: thời gian đến ngày đáo hạn

Với  N() là xác suất phân phối chuẩn tích lũy (Cumulative normal distribution function) của hai biến sau:

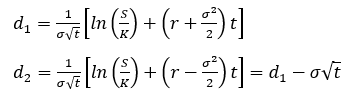
Trong đó N(di) là xác suất độ lệch trên (phải) của giá trị tham số di trong phân phối chuẩn (z). Như vậy,   

N(-d1) và N(-d2) là diện tích phía phải của hàm mật độ phân phối chuẩn.

Minh họa định giá chứng quyền

Nhà đầu tư, dự kiến mua cổ phiếu FTY tại thời điểm hiện tại với những thông tin giả đinh như sau:

Ta tính được:

CK cơ sở	FTY
So	550
K	550
	0.3
r	8%
t	0.36

N(0.25) = 0.5000 + 0.0987 = 0.5987

N(0.07) = 0.5000 + 0.0279 = 0.5279

N(-0.25) = 0.5000 – 0.0987 = 0.4013

N(-0.07) = 0.5000 – 0.0279 = 0.4721

Kết quả tính toán giá chứng quyền có bảo đảm như sau:

C = 550(0.5987) – 550[e^(-0.08*0.36)](0.5279 = 47.184

P = 47.184 – 550 + 550[e^(-0.08*0.36)]       = 31.570

Có thể bạn quan tâm:

Giá chứng quyền thay đổi thế nào khi chia cổ tức?

Cách đầu tư chứng quyền

Chứng quyền có bảo đảm là gì

Các bài viết liên quan

5 đặc điểm của nhà đầu tư chứng khoán "hệ tâm linh"

HSC Online ra mắt bộ Hướng dẫn đầu tư Chứng quyền cho người mới bắt đầu

Chứng quyền MBB và các thông tin chi tiết

Cách đọc bảng giá chứng quyền có bảo đảm

Chiến lược đầu tư chứng quyền: Đa dạng hóa và Long short investment (Phần 3)

Hướng dẫn cách đầu tư chứng quyền từ A đến Z